|
 |
|
| 単位 | 数学 | 力学Ⅰ | 力学Ⅱ | 材料力学 | 締結 | 軸 | 軸受 | 伝動 | 電気 | 図面 | 共通資料 |
| ( 戻る ) ( ホーム ) |
|
|
|
|
 |
|
|
捻り剛性(ねじりごうせい) |
|
|
|
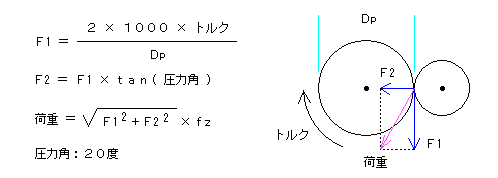
■ 軸荷重 ( 歯車駆動 )
・トルク‐ピッチ径‐歯車係数より軸荷重を計算
■ 軸荷重 ( ベルト駆動 )
・トルク‐ピッチ径‐伝動ベルト係数より軸荷重を計算
■ 軸荷重 ( チェーン駆動 )
・トルク‐ピッチ径‐チェーン係数より軸荷重を計算 |
□ 歯車係数
・歯車精度に対する補正係数(Fz)
□ ベルト係数
・初期張力(ベルトの張り)に対する補正係数(Fb)
□ チェーン係数
・振動衝撃に対する補正係数(Fc) |
| ( 歯車駆動 ) |
|
 |
|
|
|
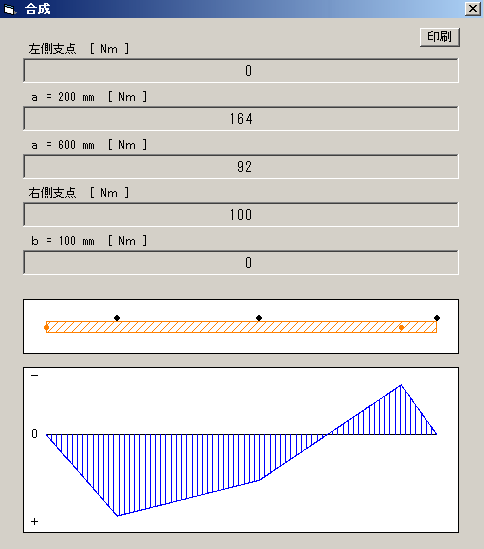
■ 軸の曲げモーメント
[ 角度指定なし ] [ 角度指定あり ]
・荷重の位置と角度‐軸受の間隔より最大曲げモーメントを計算
・軸のたわみ量は ■ 材料力学 ■ 梁のたわみ で計算可能です。
・複合計算は 記録領域を範囲指定 → [ 合成 ] ボタンをクリック ( グラフを表示
) |
|
| ( 軸の支点・荷重点に於ける合成曲げモーメント ) |
|
 |
|
|
|
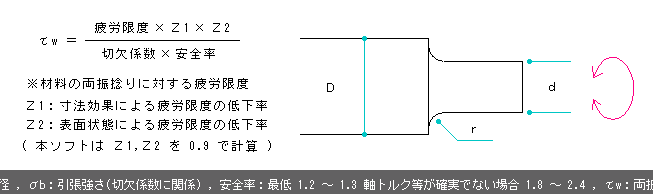
■ 段付き軸の許容応力
[ 回転曲げ ] ・大小軸径‐面取‐引張強さ‐回転曲げ疲労限度より切欠係数と許容応力を計算
[ 両振捻り ] ・ 〃 両振捻り疲労限度より
〃
※段落ち切欠部の疲労を考慮した許容応力 ( 軸径を極力小さくしたい場合に本許容応力を用いて計算
)
軸荷重やトルクが不確実な場合や腐食等が予測される場合は ■ 材料力学
◎ 許容応力 ( 参照入力 )
を推奨 |
◎ 疲労限度
[ 回転曲げ ] [ 両振捻り ] ・材料の引張強さと疲労限度
( SS400‐S10C~S55C )
・資料に含まれない材料の疲労限度は
引張強さの比較で類推ください。 |
|
| [ 両振捻り ] |
|
 |
|
|
|
■ 軸径 ( トルクを受ける場合 )
・トルク‐許容捻り応力より必要軸径を計算 → 標準軸径を選定
・通常、伝動軸はトルクと曲げモーメントを同時に受けます。
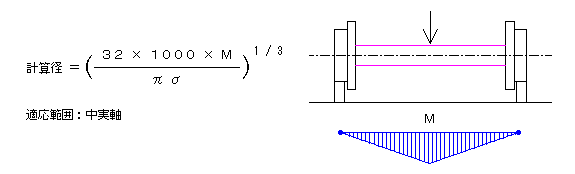
■ 軸径 ( 曲げモーメントを受ける場合 )
・曲げモーメント‐許容曲げ応力より必要軸径を計算 → 標準軸径を選定
・支持構造や荷重位置には関係しません。( 曲げモーメントの計算で加味します
)
■ 軸径 ( トルクと曲げモーメントを受ける場合 )
・トルク‐許容捻り応力‐曲げモーメント‐許容曲げ応力より相当曲げ(捻り)モーメント‐必要軸径を
計算 → 標準軸径を選定
※ ■ 材料力学 ■ 断面二次モーメント (I) , 断面係数 (Z) →
■ 円断面 ( 中空 )
[ 等価中空円 I,Z,Ip,Zp ] で
本計算値と同等の中空軸寸法を計算可能です。 |
|
| ( 曲げモーメントを受ける場合 ) |
|
 |
|
|
|
■ 軸のたわみ量
・荷重‐軸長‐軸径‐縦弾性係数(E)より断面二次モーメントと最大たわみ量を計算 |
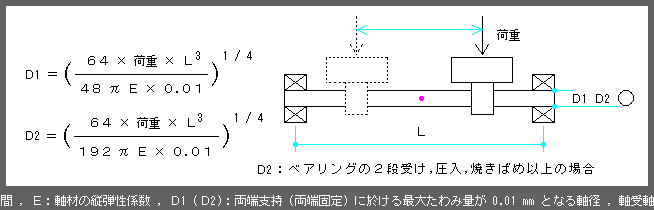
■ 曲げ剛性を考慮した軸径 ( 精密機器 )
・荷重‐軸長‐縦弾性係数(E)より最大たわみ量が 0.01 mm となる軸径を計算 → 標準軸径を選定 |
■ 軸のねじれ角
・トルク‐軸長‐軸径‐横弾性係数(G)より断面二次極モーメントとねじれ角を計算 |
■ 捻り剛性を考慮した軸径 ( 精密機器 )
・トルクと横弾性係数よりねじれ角が ( 軸長 1m 換算で ) 0.25 度となる軸径を計算 → 標準軸径を
選定 |
|
| ■ 曲げ剛性を考慮した軸径 ( 精密機器 ) |
|
 |
|
|
|
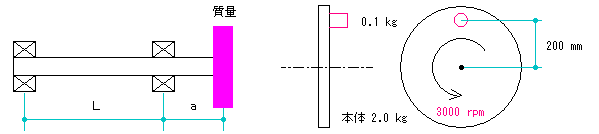
■ 軸の危険回転数
[ 集中荷重:軸受の内側 ] [ 集中荷重:軸受の外側 ] [ 分布荷重 ]
・軸径‐質量(工学単位系は荷重)‐軸の長さ‐縦弾性係数(E)より軸の断面二次モーメントと危険回転数
を計算します。
・同一要素(同一画面)での複合計算は 記録領域を範囲指定 → [ 合成 ] ボタン
異なる要素の複合計算は ■ 数学 ■ 逆数計算 [ 1/X^2 ] で X1,2,3,...
を用いて計算ください。
計算値Xが危険回転数になります。
・回転体の重心が軸心でない場合は 偏心物体の遠心力より計算します。 |
|
| [ 集中荷重:軸受の外側 ] 偏心荷重に対する軸径 ( 補足説明の計算例 ) |
|
 |
|
|
|
□ 標準軸径
・円筒軸端と軸受軸径 |
|
|
|
| 単位 | 数学 | 力学Ⅰ | 力学Ⅱ | 材料力学 | 締結 | 軸 | 軸受 | 伝動 | 電気 | 図面 | 共通資料 |
|
| ( 戻る ) ( ホーム ) |
|